What happens when you make a quadrilateral (a four sided object) and connect the midpoints of each side? What if you did this over and over again?
Here is an activity that investigates that!
Wacky Quadrilaterals
- Draw any quadrilateral that takes up most of the page. Measure the interior angles and add them all together and record this. Measure and record the perimeter
- Measure and determine the midpoint of each line. Connect the midpoints and make a new quadrilateral. (Iteration 1) Measure the interior angles of the new quadrilateral and perimeter.
- Repeat step 2, and fill in the chart with the sum of the new angles and perimeter.
- Estimate what the sum of the angles and perimeter will be the for 10th shape. (Do not make the 10th shape, simply estimate based on the pattern).
- Color in your shape to make a creative design.
What do you notice? Wonder? What would be the sum of the interior angles of iteration 10? Perimeter?
Here is a recording sheet.
A possible example:
Extension:
Simply show this animation and ask "What is this visually proving?"
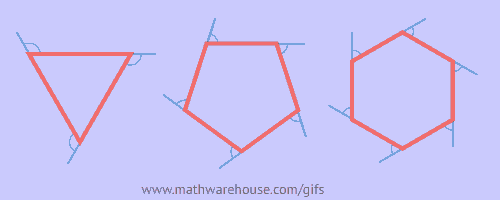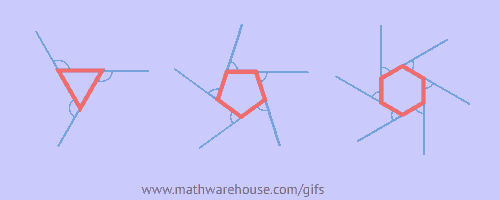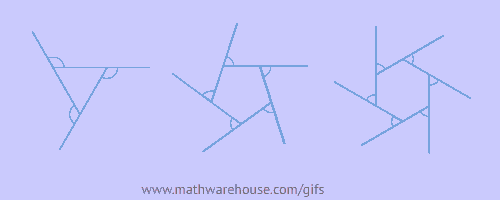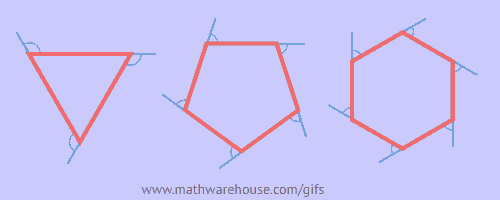
A possible video to show is here:

I love problems/tasks that "have legs". These problems can be re-experienced by students to become richer and deeper in their exploration and analysis. In senior grades, if you created ordered pairs: (figure number, sums of the lengths of the sides) as you do the constructions using the midpoints. what do you think the graph would look like? Your justification? OK -- now test your conjecture.
ReplyDeleteGreat task.
Such a great information about Wacky Quadrilaterals in this article. I got a lot of information. thanks for sharing this article with us. Now it's time to avail jupiter florida airport for more information.
ReplyDeleteFind top high DA PPT submission sites for better online visibility. Boost your SEO with these trusted platforms. They are easy to use and perfect for increasing your site's ranking.
ReplyDelete