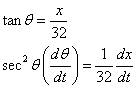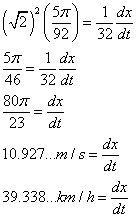2
I used to believe there was a dichotomy between science and religion. It seemed in the past, that when science could not explain why something was true, we turned to religion and simply attributed to God. There have also been arguments against the existence of a God,
from The problem of Evil to Michael Martins proof, A Disproof of Gods Existence. Even after growing up in a Catholic home, I believed that one person was either religious or logical and scientific, but not both; a Venn-diagram with no overlap. 8 years ago, this all changed when I started teaching at Notre Dame; a Catholic high school. When I make references to Church and Religion, I will be referring to the Catholic Church.
Once I started working at Notre Dame, I met many Catholic Science teachers and was shown that you can be a Catholic logical thinker. My eyes were opened to the reality that this Venn-Diagram does have an overlap. I believe, like others in the past, I did not understand the implications that Religion has on Science and also how Science impacts Religion. I will show, through my own stories how Science and Religion can, and do, coexist.
When I first started teaching Science, I was worried I would go against the teachings of the Church when I started to address the age of our Planet. Before, I took the literal sense of the Word in the book of Genesis which stated that the Earth was formed in six days, some 6000 years ago. Science has shown that the Universe is around 15 Billion years old. An obvious contradiction! After some research, on how I will address this in my Science Class, I read Frank Sheed (1982) say
"one shouldnt be forced to choose between evolution and creation."
and he continues on to say that
"Creation answers the question why does everything exist, why there isnt nothing? While evolution, is a theory, as to how come the Universe did develop once it existed." (Pg. 58)
As well, when Genesis was written, humanity did not fully understand the workings of the universe and these six days just corresponded with the Babylonian creation myth Enuma Elish, and does not really mean God created the Earth in six day at all. Religion now fully accepts the fact the Earth is not 6000 years old and that uses science to determine when God created the Universe
One discussion which arose in my class was around the idea of evolution for Apes versus the creation of humans by God. Again, before looking deeper I believed these were two contradictory ideas, but instead they are not. The Church has said it is not against the idea of evolution, and in fact evolution exists in our current era (Some people will not grow molars), and that the evolution of the body is an almost certain fact. However, religion teaches us that the soul, in which is inside our body, was not the result of any certain evolution but instead infused by God Himself; again not contradictory, but two theories from the same thread of truth.
Due to the limit of words I will not go further into detail, but science and religion also agree on when life starts, how pre maritial sex will lead to increased divorce rates, and many other theories. Science and religion are both logical, deal with science and fact, and truthfully it is
because of Science that my faith is strong.