Catching speeders from our math class
Instead of using a worksheet, or pseudo-context question
from a textbook you can show how related rates can be used to estimate the
speed of a car from our classroom window.
1)
I used the Distmeasure app to determine the
distance my classroom window is from the road.
2)
A student extended his arm and followed a car
with arm until it hit a 45 degree angle.
Different students timed how long it took and we averaged the
times. [This will allow us to calculate
the average rate of change of his arm in radians/second] in our class this took
4.6 seconds, as the following:
3)
Perform the calculations below
Since we know that student stopped at 45 degrees we can use the special triangle of 45/45/90 to substitute into the above formula.
4)
Talk about the limitations of this activity, and
how accurate this is.
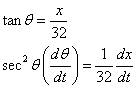
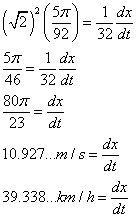
It is the most important topic which has a great role in research work of mathematics.Calculus (Latin, calculus, a small stone used for counting) is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem of calculus. Calculus is the study of change,[1] in the same way that geometry is the study of shape and algebra is the study of operations and their application to solving equations.
ReplyDeletecool! sounds like a fun party trick too.
ReplyDelete